Trigonometry is one of the most important topics of Mathematics and when it comes to trigonometry, then many students feel difficulty in learning all the formulas of trigonometry. So, one thing is very important to realize here and that is: “Focus on learning the basic identities and basic formulas”. All other formulas can be deduced with the help of these. Now the question arises what these Basic Identities of Trigonometry and Basic Formulas are? So, here is a step-by-step explanation for all such questions.
Trigonometry will be the part of mostly all the defence exams like NDA exam, CDS Exam, INET, Territorial Army, Group X and Y and more, so if you are preparing for the defence exams, make sure you go through these Trigonometry formulas to better understand the concepts that will help you the solve questions in Maths exams.
Now to get started let us start with noting the difference between Trigonometric identities and Trigonometric Ratios.
- Trigonometric Identities are some formulas that involve trigonometric functions. These trigonometry identities are true for all values of the variables.
- Trigonometric Ratio is known for the relationship between the measurement of the angles and the length of the side of the right triangle.
Trigonometry is a branch of mathematics that deals with the relationships between the sides and angles of triangles. Here are some of the important formulas in trigonometry:
- Pythagorean theorem: a² + b² = c² This formula relates the lengths of the sides of a right-angled triangle, where a and b are the lengths of the legs and c is the length of the hypotenuse.
- Sine formula: sin A/a = sin B/b = sin C/c This formula relates the sides and angles of any triangle, where A, B, and C are the angles, and a, b, and c are the opposite sides to these angles.
- Cosine formula: a² = b² + c² – 2bc cos A This formula relates the sides and angles of any triangle, where A is the angle opposite the side a, and b and c are the other two sides.
- Tangent formula: tan A = sin A/cos A This formula relates the tangent of an angle to the sine and cosine of the same angle.
- Cosecant formula: csc A = 1/sin A This formula relates the cosecant of an angle to the sine of the same angle.
- Secant formula: sec A = 1/cos A This formula relates the secant of an angle to the cosine of the same angle.
- Cotangent formula: cot A = 1/tan A = cos A/sin A This formula relates the cotangent of an angle to the sine and cosine of the same angle.
Remembering these formulas can help you solve a wide range of trigonometric problems, including finding the missing sides and angles of a triangle, as well as working with functions such as sine, cosine, and tangent.
Trigonometry is a very important topic in mathematics, and it is essential to learn the basic identities and formulas to excel in this subject. Here are some of the basic identities and formulas of trigonometry:
- Pythagorean identity: sin²θ + cos²θ = 1 This identity shows that the sum of the squares of the sine and cosine of an angle is always equal to one.
- Cofunction identity: sin(90° – θ) = cosθ and cos(90° – θ) = sinθ This identity shows that the sine of the complement of an angle is equal to the cosine of the angle, and the cosine of the complement of an angle is equal to the sine of the angle.
- Reciprocal identities: sinθ = 1/cscθ cosθ = 1/secθ tanθ = 1/cotθ These identities show the reciprocal relationship between the trigonometric functions and their inverses.
- Quotient identities: tanθ = sinθ/cosθ cotθ = cosθ/sinθ These identities show the relationship between tangent and cotangent and sine and cosine.
- Even-odd identities: sin(-θ) = -sinθ and cos(-θ) = cosθ These identities show that the sine function is an odd function and the cosine function is an even function.
- Sum and difference identities: sin(θ ± φ) = sinθ cosφ ± cosθ sinφ cos(θ ± φ) = cosθ cosφ ∓ sinθ sinφ These identities show the relationship between the trigonometric functions of the sum or difference of two angles and the trigonometric functions of the individual angles.
- Double angle identities: sin2θ = 2sinθ cosθ cos2θ = cos²θ – sin²θ These identities show the relationship between the trigonometric functions of double an angle and the trigonometric functions of the individual angles.
- Half angle identities: sin(θ/2) = ±√[(1 – cosθ)/2] cos(θ/2) = ±√[(1 + cosθ)/2] These identities show the relationship between the trigonometric functions of half an angle and the trigonometric functions of the original angle.
Now let us start with the basic formulas of trigonometry and see the basic relationships on which the whole concept is based on.
We have six trigonometric ratios: sine, cosine, tangent, secant, cosecant and cotangent known as sin, cos, tan, sec, cosec and cot respectively. These all are measured by taking the ratios of sides of a right-triangles. Here is the list of each ratio in term of angle ‘x’:

Trigonometric Identities:
After knowing these angles, first thing which one should know are the Trigonometric Identities. They will be used most of the time.
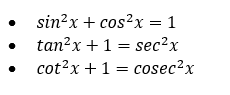
Allied Angles:
Two angles are said to be allied when their sum or difference is either zero or a multiple of 90.

The angles like -. Let’s discuss the important allied angles only. The following conversion in sign is due to change in quadrant.


Trigonometric Ratios of Sum and Difference of Two Angles:

Product of Sum and Difference of Angles:
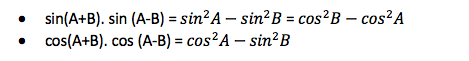
Transformation of Product into Sum or Difference:
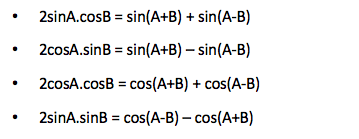
Transformation of Sum or Difference into Products:

If these formulas are at your tips, then trigonometry will not be any trouble for you. You will be able to derive many more formulas with the help of these. Do not forget to watch my lectures on trigonometry if you are preparing for the defence exams. Download SSBCrackExams Learning App now!














